Plonger dans le monde des mathématiques peut parfois sembler déroutant, en particulier lorsqu’il s’agit de concepts comme les nombres relatifs. Ces chiffres, à la fois positifs et négatifs, sont essentiels dans de nombreux aspects quotidiens, que ce soit dans les finances ou même lors de la prise de température. Une méthode efficace pour appréhender ces concepts complexes est l’utilisation des cartes mentales. En facilitant la visualisation, elles permettent aux élèves de décortiquer les informations et de mieux assimiler ces notions. Dans cet article, nous explorerons comment créer et utiliser des cartes mentales pour maîtriser les nombres relatifs.
Qu’est-ce qu’une carte mentale ? Un outil essentiel pour l’apprentissage
Avant de nous pencher sur les techniques spécifiques d’utilisation des cartes mentales pour les nombres relatifs, il est important de définir ce qu’est réellement une carte mentale. C’est un outil graphique qui permet d’organiser les concepts autour d’un thème central. Cette méthode visuelle stimule la créativité et aide à établir des relations logiques entre les idées.
Les cartes mentales se caractérisent par :
- Visualisation dynamique : La représentation graphique rend l’information plus accessible.
- Engagement actif : En créant une carte, l’élève participe activement à son apprentissage.
- Structure flexible : Contrairement à des notes linéaires, les cartes permettent de structurer les idées selon la perception de l’élève.
En mathématiques, surtout lors de l’étude des nombres relatifs, cet outil devient précieux. Visualiser les relations entre ces nombres contribue à leur compréhension. Par exemple, un élève qui souhaite assimiler la notion de positifs et négatifs peut créer une carte mentale qui illustre les concepts des opposés et de la distance à zéro.
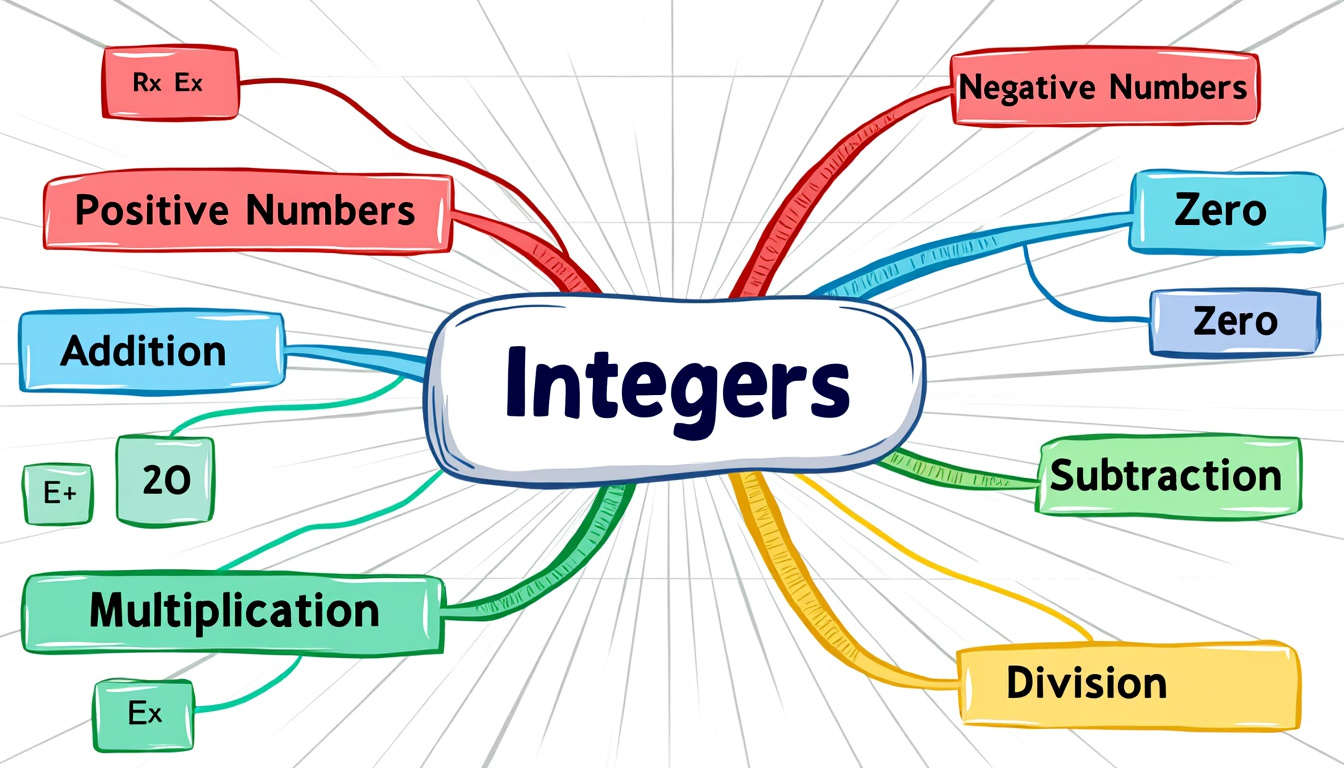
Les avantages des cartes mentales dans l’apprentissage des nombres relatifs
Les cartes mentales se révèlent particulièrement efficaces lors de l’apprentissage des nombres relatifs, une notion fondamentale des mathématiques. Ces avantages sont essentiels pour améliorer l’expérience des élèves. Parmi eux, on peut citer :
- Facilitation de la compréhension : Visualiser les notions aide à saisir facilement des opérations comme l’addition et la soustraction.
- Amélioration de la révision : Elles offrent un résumé clair des concepts, idéales pour réviser avant un examen.
- Stimulation de la créativité : Créer une carte demande une implication active, ce qui motive davantage les élèves.
Par exemple, un élève révisant pour un contrôle peut synthétiser ses connaissances sur les propriétés des nombres relatifs. En reliant les règles d’addition aux exemples pratiques, il ancre les notions de manière intuitive. Cela lui permettra de mieux se souvenir des opérations à réaliser.
Créer une carte mentale : étapes à suivre pour une efficacité maximale
La création d’une carte mentale efficace est un processus méthodique qui nécessite des étapes clés. Voici comment élaborer une carte mentale efficace sur les nombres relatifs :
Étape 1 : Définir le thème central
Le premier pas consiste à déterminer le thème central de votre carte. Pour ce sujet, le thème sera « Nombres Relatifs ». Positionnez ce thème au centre de votre feuille ou sur une plateforme numérique.
Étape 2 : Identifier les concepts clés
Identifiez les concepts principaux que vous souhaitez inclure, tels que :
- Désignation des nombres : Positifs et négatifs
- Propriétés : Opposés, distance à zéro
- Opérations : Addition, soustraction, multiplication, division
Étape 3 : Établir des branches
À partir de ces concepts, dessinez des branches s’étendant à partir du thème central. Chaque branche peut contenir des sous-thèmes ou des détails supplémentaires. Par exemple, « Opérations » pourrait inclure des sous-catégories pour chaque type d’opération.
Étape 4 : Intégrer des couleurs et des symboles
Améliorez la lisibilité en utilisant des couleurs différentes pour chaque branche et en ajoutant des symboles pertinents. Cela renforce la mémorisation des concepts associés.
Étape 5 : Réviser et enrichir votre carte
Relisez votre carte et apportez des ajouts, comme des exemples ou des anecdotes. Par exemple, pour l’addition, vous pourriez illustrer avec 5 + (-3) = 2 pour montrer l’impact des signes.
Comprendre les propriétés des nombres relatifs via la carte mentale
Une section cruciale de votre carte mentale concerne les propriétés des nombres relatifs. Ces propriétés incluent :
Signes des nombres
Les nombres peuvent être soit positifs, soit négatifs. Cette dualité doit être bien représentée sur votre carte :
- +3 est un nombre positif.
- -5 est un nombre négatif.
- Distance à zéro : La valeur absolue aide à comprendre cette distance.
Comparaison
Intégrez aussi la comparaison entre ces nombres. Indiquez que tout nombre positif est supérieur à tout nombre négatif, ce qui peut être illustré avec un exemple pratique, comme :
Pour comparer 2 et -3, on constate que 2 > -3.
Opposés
Les nombres opposés doivent également être mentionnés. Cela montre qu’une symétrie existe autour de zéro, par exemple :
- +7 et -7 sont des opposés.
- +10 et -10, pareillement.
| Propriété | Description |
|---|---|
| Signe | Indique si un nombre est positif ou négatif. |
| Distance à zéro | Représentée par la valeur absolue d’un nombre. |
| Opposés | Deux nombres ayant la même valeur absolue mais des signes opposés. |
Les opérations avec les nombres relatifs : comment les visualiser efficacement
Une carte mentale doit aussi inclure les différentes opérations mathématiques impliquant les nombres relatifs. Ces opérations suivent des règles spécifiques que l’élève doit comprendre.
Addition
Lors de l’addition de deux nombres relatifs :
- Si les signes sont les mêmes, additionnez les valeurs et conservez le signe.
- Si les signes sont différents, soustrayez les valeurs et conservez le signe du nombre ayant la plus grande valeur absolue.
Soustraction
La soustraction peut également être envisagée comme l’addition d’un opposé :
A – B = A + (-B)
Multiplication et Division
Il est important de se rappeler que :
- Deux nombres de même signe donnent un résultat positif.
- Deux nombres de signes opposés donnent un résultat négatif.
| Type d’Opération | Exemple | Résultat |
|---|---|---|
| Addition | 8 + (-5) | 3 |
| Soustraction | 10 – 3 | 7 |
| Multiplication | 2 × (-3) | -6 |
Exploiter les cartes mentales pour les révisions des nombres relatifs
Une fois que vous avez défini votre carte mentale, il est essentiel de l’utiliser efficacement lors de vos révisions. Voici des conseils pratiques :
- Lecture active : Lisez votre carte à voix haute pour ancrer les concepts dans votre mémoire.
- Exercices pratiques : Utilisez-la pour résoudre divers exercices sur les nombres relatifs.
- Partage en groupe : Discutez des concepts avec des camarades pour enrichir votre compréhension.
- Révisions régulières : Planifiez des séances de révisions pour redessiner votre carte de mémoire.
Ces actions renforceront vos connaissances et votre confiance lors des évaluations. Par exemple, après avoir examiné votre carte, résolvez des problèmes tels que :
5 + (-2) = ? et -3 – 4 = ?
Ressources numériques pour créer des cartes mentales
Avec l’explosion des technologies, diverses plateformes en ligne facilitent la création de cartes mentales. Voici quelques-unes des plus recommandées :
- MindMeister : Idéal pour collaborer en temps réel.
- XMind : Interface intuitive avec des options avancées.
- Canva : Parfait pour des designs élaborés.
- Bubbl.us : Simple et efficace pour des cartes basiques.
- Mindomo : Prémium et fonctionnel pour des tâches complexes.
Utiliser ces outils peut simplifier le processus de création et stimuler l’engagement des élèves, rendant l’apprentissage des nombres relatifs plus ludique.
Questions fréquentes sur les cartes mentales et les nombres relatifs
Voici quelques réponses aux questions que se posent souvent les élèves concernant les cartes mentales et les nombres relatifs :
Pourquoi utiliser des cartes mentales pour réviser les nombres relatifs ? Les cartes mentales aident à structurer les informations, facilitant ainsi la compréhension et la mémorisation.
Quels outils numériques recommandez-vous ? Des plateformes comme MindMeister, XMind et Canva sont excellentes pour créer des cartes facilement.
Une carte mentale peut-elle aider à résoudre des problèmes mathématiques ? Oui, elle sert de référence visuelle, renforçant la confiance lors des exercices.
Vaut-il mieux dessiner à la main ou utiliser un logiciel ? Cela dépend des préférences. Les deux ont leurs avantages en termes de mémorisation et d’organisation.
Combien de temps prend la création d’une carte mentale efficace ? Cela varie selon la complexité, mais il est crucial de ne pas se précipiter.









